How many times a day a clock's hands overlap?
Using Javascript, as a software developer I'll try to answer interview question "How many times a day a clock's hands overlap?" with the exact overlapping times of the clock's hour hand and minute hand. This tricky question was asked by my manager to one of our intern university student. Later we learnt that this question "How many times do a clock's hands overlap in a day?" is an interview question asked for job applicants in Google.
Let's first analyze the problem of overlapping clock's hour and minute hands. First set our imaginary clock to 12:00 midnight which is the starting time for the problems time period.
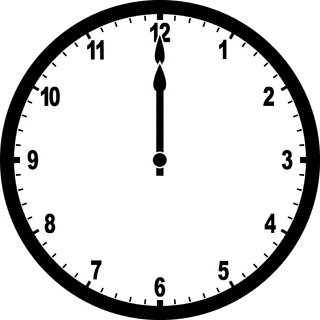
As you see at start time when the period for calculation starts we have an overlapping condition for clock's hour hand and minute hand.
Now assume that the clock's hour and minute hands overlap for the next time. The first overlapping after 12:00 o'clock will happen between 1 o'clock and 2 o'clock. But we do not know the exact time right now at this stage of the problem solution.

Let's examine the above situtation now. First of all, clock's hour hand only moved from position 12 to a position between 1 and 2. What is interesting for the solution of this inteview question is that at the same time period, the minute hand of the clock completed a full cycle starting from 12 to 12 and additionally traveled the same distance as hour hand at the overlapping time.
Here is a drawing displaying the case visually to help you understand the hint for the solution of "how many times a day a clock's hands overlap?".
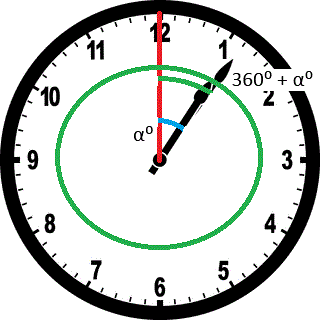
We have one base mathematical equation for this problem that will lead us to solution. The minute hand is 12 times faster than the hour hand. If you think of the time passing from 12:00 o'clock to 1 o'clock, the minute hand travels 360 degrees. On the other hand the hour hand travels 1/12 of 360 degrees. Or in a different thinking, in a specific time period (t) minutes, the minute hand travels (360 * t) / 60 degrees But at the same time the hour hand only travels 1/12 of that degree: (360 * t) / (60 * 12) degrees.
An other equation comes from the passed hours. Each passing hour the minute hand completes a full cycle. Let's say that the hour hand traveled (n) degrees. So we can say at when they overlap each other the minute hand traveled (360 + n) degrees at the same time as hour hand.
So we can now say that while hour hand travels (n) degrees the minute hand will travel (12*n) degrees. The result that will outcome from this additional equation with first mathematical equation will be as follows:
12 * n = 360 + n
Of course 360 degrees is true if only 1 hour has passed.
If two hours passed, then the formula will be: 12 * n = 360*2 + n
So we can re-formulate the equation as follows:
12 * n = 360 * h + n
Now replace n the degree the hour hand traveled in time t, (360*t)/(60*12)
12 * (360*t)/(60*12) = 360 * h + (360*t)/(60*12)
11 * (360*t)/(60*12) = 360 * h
11 * t / 2 = 360 * h
11 * t = 720 * h
For first hour we can replace h with 1 and we can solve the equation for first overlap after 12:00 o'clock
t = 720 /11 = 65,45 minutes
There is an other tricky conversion here the decimal part of the time. We need to convert it to seconds.
0,45 minutes = 45/100 minutes = 45*60/100 seconds= 27 seconds
So the first overlap is at 65 minutes 27 seconds later which means 1:05:27
Then we can continue calculation for the second overlap of clock's hands. This will occur between 2 o'clock and 3 o'clock. This means minute hand of the clock will travel 2 times full circle and plus the same amount as hour hand.
Now I want to move all these calculations into below Javascript code
Javascript Code
Here are some sample Javascript codes calculating the times when the clock's hands overlap in a day
Please note that the below Javascript code is provided by Hilal �etinkaya, our intern student. Thanks a lot for her help for the solution of this interesting problem.
There is a Javascript Loop structure to calculate each time the minute hand completes a full cycle. Since in a day the pattern from midnight till noon will be same for the second half of the day (from noon till midnight), the Javascript loop is defined for an integer variable starting from 0 to 11.
var t, n, temp1, temp2;
var hour, minutes, seconds;
for (t = 0; t < 12; t++) {
n = 720 * t / 11;
var n = Math.round(n * 100) / 100;
hour = Math.floor(n / 60);
minutes = Math.floor(n) % 60;
temp1 = n * 100;
temp2 = temp1 % 100;
seconds = Math.floor((temp2 * 60) / 100);
document.write( (t+1) + ". time overlap occurs at " + hour + ":" + minutes + ":" + seconds + "
");
}
Within the loop, each overlap condition is calculated using the mathematical equation discussed in previous section. For loop structure contains mod functions and Mart.floor() functions for converting the time in minutes to hours:minutes:seconds display format.
As you see in the output of this sample Javascript code, first overlap occurs at 00:00:00 o'clock.
And the last overlap of clock's hand will occur at 24:00:00
To answer the interview question "How many times a day a clock's hands overlap?", first of all we should determine if first overlap time that is the starting time counts or not.
I assume that we can agree the start time is also one of the overlapping times in a day.
So, here is the times count and clock's hands overlap times within 24 hours:
1. time overlap occurs at 00:00:00
2. time overlap occurs at 01:05:27
3. time overlap occurs at 02:10:54
4. time overlap occurs at 03:16:21
5. time overlap occurs at 04:21:49
6. time overlap occurs at 05:27:16
7. time overlap occurs at 06:32:43
8. time overlap occurs at 07:38:10
9. time overlap occurs at 08:43:38
10. time overlap occurs at 09:49:05
11. time overlap occurs at 10:54:32
12. time overlap occurs at 12:00:00
13. time overlap occurs at 13:05:27
14. time overlap occurs at 14:10:54
15. time overlap occurs at 15:16:21
16. time overlap occurs at 16:21:49
17. time overlap occurs at 17:27:16
18. time overlap occurs at 18:32:43
19. time overlap occurs at 19:38:10
20. time overlap occurs at 20:43:38
21. time overlap occurs at 21:49:05
22. time overlap occurs at 22:54:32
23. time overlap occurs at 24:00:00 (since we count starting as one of overlaps, this might be excluded)
As a result, if you count the last case, there are 23 times when a clock's hour and minute hands overlap in a day. If you exclude one of the midnights, we can conclude that there are 22 times when a clock's hands overlap in a day.
